Asal sayılar matematik dersinin temel konularından biridir, YKS TYT AYT KPSS DGS gibi sınav türlerinde de karşımıza çıkan önemli konulardandır. Aşağıda asal sayı nedir, özellikleri ve türleri nelerdir gibi sorularınızın cevabını bulabilirsiniz;
Asal Sayılar
1 den ve kendisinden başka pozitif böleni (çarpanı) olmayan 1 den büyük doğal sayılara asal sayılar denir.
Asal olmayan ve 1 den büyük olan doğal sayılara bileşik sayı denilir. İlk 10 asal sayı; 2, 3, 5, 7, 11, 13, 17, 19, 23, 29 dur. ilk 10 bileşik sayı ise; 4, 6, 8, 9, 10, 12, 14, 15, 16, 18 dir.
2 den başka çift olan asal sayı yoktur.
Asal sayılar kümesi üstten sınırsızdır.
1 den büyük her doğal sayının en az bir asal sayı çarpanı (böleni) vardır.
n bir bileşik sayı ise n sayısının √n den büyük olmayan bir asal çarpanı vardır. Bu özellik nedeniyle herhangi bir n doğal sayısının asal sayı olup olmadığı şöyle anlaşılır:
- n sayısının √n den küçük eşit olan asal sayılardan en az birine bölünüp bölünmediği kontrol edilir. Hiçbirine bölünemiyorsa, n asal sayıdır.
ÖRNEK
- 223 sayısı asal sayıdır. Çünkü, √223 – 14,9… dur. 14,9… e kadar olan asal sayılar; 2, 3, 5, 7, 11 dir. 223 sayısı bu asal sayılardan hiçbirine bölünemez. O halde, 223 asal sayıdır.
Asal Çarpanlarına Ayırma
1 den büyük her tam sayı, tabanları farklı asal sayılar, üsleri pozitif doğal sayılar olan çarpanlar cinsinden, çarpanların yazılış sırası önemli olmamak üzere tek türlü yazılabilir. Bu yazılıma, o sayının asal çarpanlarına ayrılması denir.
ÖRNEK
n! Sayısının Çarpanlarının Üssünü Bulmak;
m≤n ve m asal sayı olsun. n! sayısı asal çarpanlarına ayrıldığında m nin üssü şöyle bulunur:
[alert type=”info” icon-size=”normal”]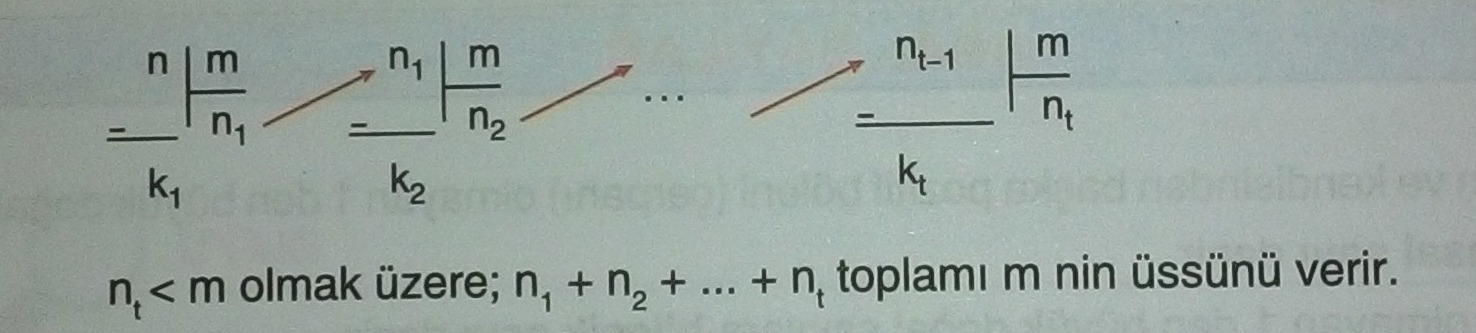
[/alert]
n! Sayısının Sonundaki 0 Sayısı;
n≥25 olmak üzere, n! sayısının sonunda ardışık olarak kaç tane 0 olduğu şöyle bulunur:
[alert type=”info” icon-size=”normal”]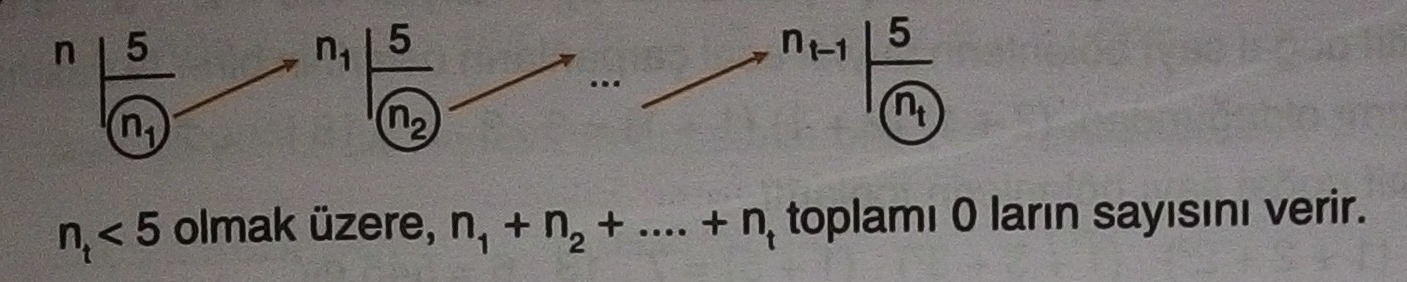
[/alert]
UYARI
- n≥25 için n! – 1 sayısının sonundaki ardışık 9 ların sayısı, n! sayısının sonundaki 0 ların sayısına eşittir.
Bir Doğal Sayının Tam Sayı Bölenleri;
a, b, c, … birbirinden farklı asal sayılar; p, q, r, … pozitif doğal sayılar olmak üzere, n≥2 doğal sayısı; n = biçiminde asal çarpanlarına ayrılmış olsun.
1. n doğal sayısının pozitif tam sayı olan bölenlerinin sayısı;
- (p + 1) (q + 1).(r + 1)… dir.
n doğal sayısının bütün tam sayı bölenlerinin sayısı;
- 2.(p+1)(q + 1).(r + 1) … dir.
2. n doğal sayısının pozitif tam sayı olan bölenlerinin toplamı;
- [alert type=”info” icon-size=”normal”]
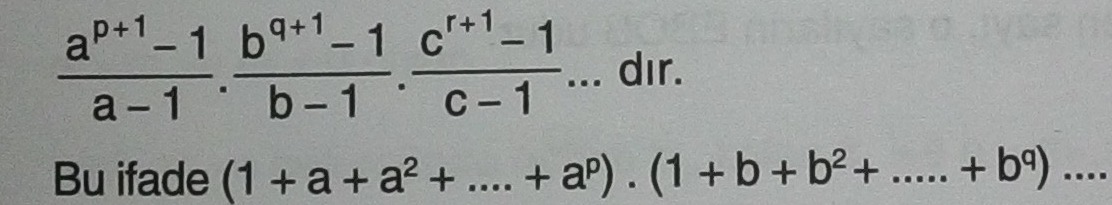biçiminde de yazılabilir.[/alert]
3. n doğal sayısının pozitif tam sayı olan bölenlerinin çarpımı;
- [alert type=”info” icon-size=”normal”]
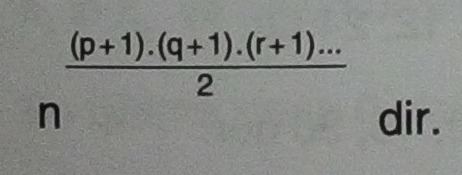[/alert]
4. n doğal sayısından küçük ve n ile aralarında asal doğal sayıların sayısı;
- [alert type=”info” icon-size=”normal”]
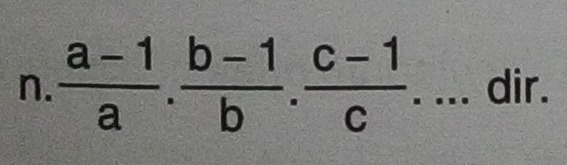[/alert]